关于监督学习的感想

"端正态度~" "仔细读题~" "快去写作业～"

暑假里似乎只做了两件事。上完了 coursera 的机器学习课程。在学车。

最初的原因是想做 chatbot，但是随着学习的深入越觉得难以实现。各种个样的因素都有。比如缺乏好的数据集，许多英文的 NLP 方法不一定适合中文等等。

暂且不说有什么实际用途，收获还是不小的。原课程地址https://www.coursera.org/learn/machine-learning/home/welcome，来自著名的 Andrew Ng。有兴趣务必去听听看。作业不是很难，但是跟着做完就会发现其实会了很多。

对于我个人而言，在机器学习本身之外的收获更大。也得以反思自己学习方式和人们的行为选择，本文不打算多说代码，以感想（没什么用的东西）为主。

其实（机器）学习是个拟合的过程，是从一个数据集中学习特定结果的得出方法。在这个课程中有几个概念贯穿到底。Features、CostFunction、Overfitting。也就是特征、成本函数、过度拟合。

以监督学习中的 Logistic Regression 举例子。

先说数学部分。例子不一定恰当请多包含。

假设我们有一个现成的，一共有 m 个样本，j 个特征的数据集用来预测某个学生是否能成功考研。

其中$(x_m^1,x_m^2,x_m^3,x_m^4...x_m^j )$分别对应这个学生的特征值。比如这个学生的 GPA，数学平均分，四六级分数，模拟考试分数……等等。而$(y_1,y_2,y_3,y_4...y_m$)则是数据集中学生是否成功的结果，可能是 0 或者 1。：

$(x\_1^1,x\_1^2,x\_1^3,x\_1^4...x\_1^j), (y\_1)$ $(x\_2^1,x\_2^2,x\_2^3,x\_2^4...x\_3^j), (y\_2)$ $(x\_3^1,x\_3^2,x\_3^3,x\_3^4...x\_3^j), (y\_3)$ $(x\_4^1,x\_4^2,x\_4^3,x\_4^4...x\_4^j), (y\_4)$ $.....$ $(x\_m^1,x\_m^2,x\_m^3,x\_m^4...x\_m^j), (y\_m)$

暂且把每一个特征的参数设定为一个$(\theta_i$) ,分别是$(\theta_1,\theta_2,\theta_3,\theta_4...\theta_i$)如果假设能够线性拟合，那么只要传入一个数据集外的学生对应的$(x^1,x^2,x^3,x^4...x^j$)数组,通过计算 $(\theta^Tx$) 即 $(\theta_1x^1+\theta_2x^2+\theta_3x^3+\theta_4x^4+...+\theta_ix^j$)就会得到一个对应的数字，将其传入 Sigmoid 函数,即计算

$h\_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$

将变量映射到 0,1 之间，然后再设置一个 threshold，比如大于 0.8，就认为可以判断为这个学生成功的可能性就很大了。

为了得到$(\theta$),先设计一个 CostFunction，在 Logistic Regression 时如下公式所示： $f(x): \begin{cases} -log(h\_\theta(x)), y = 1 \\\ \\\ -log(1-h\_\theta(x)),y = 0 \end{cases}$

合并化简可以得到 CostFunction

$J(\theta) = -\frac{1}{m}[\sum\_{i=1}^my^{(i)}logh\_\theta(x^{(i)})+(1-y^{(i)})log(1-h\_\theta(x^{(i)}))]$

使我们的函数参数在偏离数据集合时这个值变大，接近数据集合时变小。通过数据集从数学意义上来降低 CostFunction，使得函数不断的接近训练数据。常用的有 gradient descent 等，在这里不给出。

最后我们得到的类似下图中一样的分界线

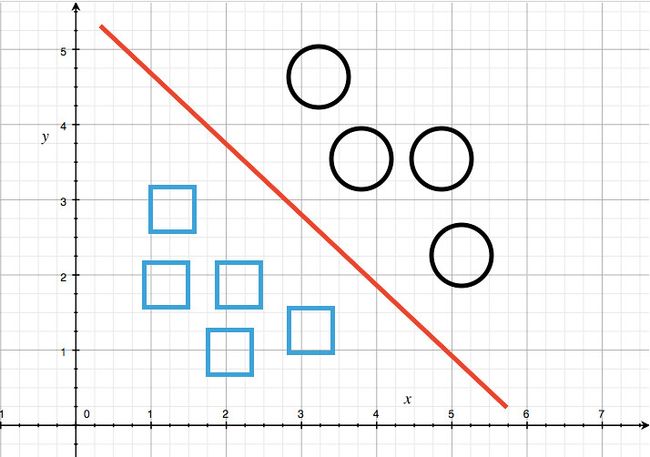
。你肯定要问为什么是线性的。显然这个世界并没有那么简单，比如这个学生恋爱的概率说不定和长相的 3 次方相关，和身高的平方相关，和 GPA 的反比有关，那么就会得到一个更加复杂的多的方程，可能是$(\theta_1x_1^{3}+\theta_2x_2^{9}+\theta_3x_1x_2x_3^{-2}+\theta_4x_4x_5^2+...+\theta_ix_i^{4}$)之类的,那么就能拟合很多的非线形情况了。

于是就到了介绍 Overfitting，也就是过度拟合的时候。图片来自 coursera 讲义 如下图所示，左边的对情况拟合不足，中间的正好，而右边的过度拟合。

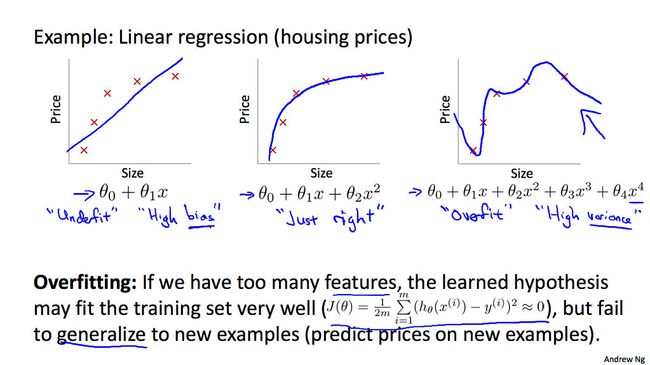
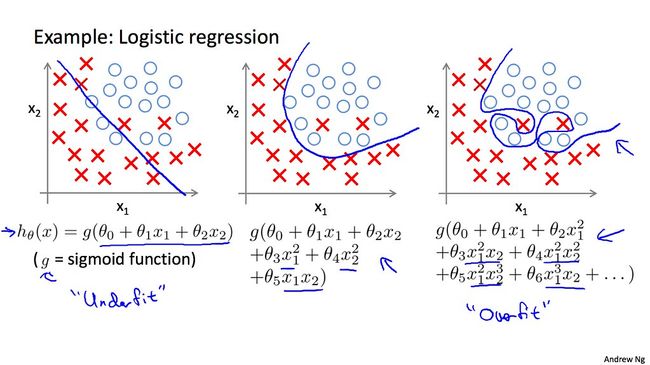为什么过渡拟合不好呢？答案是对可能的未知的数据的预测能力不足。也就背离了我们机器学习的初衷。通常的的办法有在 CostFunction 后面加上 $(\lambda\sum\_{j=1}^n\theta_j^{2}$) 提高学习$(\theta$)的成本，或是减少特征的数量，或者是提供更大的数据集。

终于到了感想时间。其实学习就是这样观察数据，得出规律，通过各种个样方法使得规律更有普遍性，降低错误率，然后用已知的规律去预测数据集外的可能性。

如果要学好什么，事实上也变的十分的清楚
1、尽可能的拥有更大的数据集 （肝）
2、学习时要有怀疑精神 （自己算）
3、更加仔细地观察数据 （用脑子）

其实我们在日常中也不得不经常面对 overfitting 的问题，比如培训机构的有多少的可信度？平时练习和正式考试是不是就是一样的题型？家长指向的未来又有多少的可信度？在 CostFunction 后的变量，事实上就是让信息提供方给出足够的证明，而不是盲目轻信。就算有题海缺没有灵活变通的能力，也只会造成巨大的浪费。同样这在另一方面也证明了无法，也没必要满足每个人的需求。

而 underfitting，一种情况是由于对数据集的观察不足，比如在结婚时，常见的参考因素有年龄、是否有房有车、是否有时间陪伴等，但是忽略某些参数，像是性格、兴趣，就说不定反而会偏离自己的愿望很远。还有一种情况是陷入了对他人的不信任，在之前追加的矫正式子中如果把$(\lambda$)设定的太高，就会像缺乏听取他人意见的能力一样而失败。

我们常说的“书呆子”，“读书读傻了”，其实就是习得了一个过渡拟合的处理方式。太过于在意书中或者他人所说的每一句话，在面对书中的内容是能够处理的非常好，但是一面对未知情况就得出了非常糟糕的结果。

如果说某个人拥有优秀的学习能力，其实就是他往往能够从数据中得出有效的主要的成分，充分使用已有的数据集，擅长归类，擅长组合信息并能够根据信息的不同情况做出合理的判断，还能够根据数据集的变化不断改进自己的想法。

假设某个数据明明给出了负面的结果，本身特征却在正面的数据集中，常用的思路就是观察这个特例和其他正面结果在特征上的区别，从中得出一些新的特征，其实也就是老师常说的“观察细节”，“仔细读题”。

懒惰的人则视他人给出的数据为无物，甚至完全不管数据集的存在，如果连课本都不看，老师说什么也不听，当然无法达成学习的目标，这也是所谓的“端正态度”。

而如果说某个老师不好，其实就是这个老师给出了不足或者错误的、无效的数据集，或者过分强调某些事实上不起决定作用的问题特征。比如在高中时某学科平时练习和正式考试往往难度不一样，这就是一种典型的提供数据集的错误。

在检验习得的模型时，也常常把数据集分成三份，一份用于训练模型，一份用于测验，一份用于模拟正式测试。是的，其实就是学校中往返进行的回家作业-月考-期末测试的过程。

在学习之前曾经觉得机器学习是什么很厉害的魔法，事实上也只是学会如何冷静的判断样本，通过数学过程产生积极的效果。

所以大家也在日常中，更加科学的训练自己的思维方式吧(~￣ △ ￣)~